Free Body Diagram Constant Velocity

Free Body Diagram Title

page 1

This text is meant to accompany grade discussions. It is not everything at that place is to know about the forces. It is meant as a prep for class. More detailed notes and examples are given in the form notes, presentations, and demonstrations (click here.)Fill out this summary sail every bit after reading each section, (click here). (Your teacher may give you a Google Apps link instead.

Introduction to Gratuitous Body Diagrams

Free body diagrams, ofttimes abbreviated "fbd" are a tool for solving problems with multiple forces interim on a single body. The methods developed hither tin can also be used for the summation of forcefulness fields. The purpose of a free torso diagram is to reduce the complexity of situation for easy analysis. The diagram is used as a starting point to develop a mathematical model of the forces acting on an object.

In order to effectively use complimentary body digram to analyze a torso's movement you must exist reach four skills.

Identify the force acting on a body
Identify the direction of each acting force and draw vectors representing the forces
Create a pair of equations from a complimentary trunk
Do the math. This ordinarily involves systems of equations.

Below is a picture of a flight jet.

Imagine how fourth dimension consuming and cluttered it would be if y'all were to draw this picture with the forces acting on the plane. It might look like the one beneath.

A free body diagram is a pic showing the forces that act on a trunk. Most chiefly it shows the forces' directions without the clutter of drawing the trunk.

The give-and-take "body" is used to describe any object. Merely physicists and engineers likes to simplify the drawing of the object by drawing a dot instead of a detailed picture. Occasionally some simple details are added to create further clarify the state of affairs. Beneath is an example of a "body."

A free body diagram of the jet might await similar the one beneath.

Weight

Weight is a term nosotros employ to depict the pull of gravity. If a physicist had defined the terms we employ everyday in our conversations with each other, then instead of "weighing 120 pounds" at the doctor's office, the doctor would instead "measure the pull of gravity as a 120 pound force."

If a trunk has mass then is has weight when it is near the surface of the Globe. Weight always pulls downward towards the middle of the Earth.

Drawing the weight's force on an gratuitous torso diagram.

On a free body diagram, "fbd," weight, "mg," is Ever drawn pulling towards the ground. The direction the trunk is moving and the other forces interim on the torso practise not alter weight's direction on a gratis body diagram.

Weight is divers at the mass of a torso times the pull of gravity. Using our math model this is written every bit

W=mg

Where "W" is the weight measured in Newtons [North.] Always utilize a Capital "N." [The letter you write must expect like the accepted capital "Due north." That means it cannot look similar a lower example "n" that is written bigger.] "m" is the mass in kilograms. "g" is the acceleration due to gravity. On the Earth'southward surface this is ix.eighty m/due south². In our arrangement of weights and measures, the unit of force is the pound. Information technology is abbreviated "lb."

In gild to have the weight force on a free torso diagram, the body must accept mass and information technology need to be on a very near a large body such as a planet.

Normal Force

The normal forcefulness is a strength that is:

perpendicular to the surface,
a reaction force to presence of other forces.

The normal force keeps two surfaces from sinking into each other. The symbol for the normal force is the Greek letter "eta." It look like a large lower case "n" with a tail.

Currently you are sitting downward or standing. The ground experiences a force pulling y'all down. The normal strength is perpendicular to the surface and is a reaction to the force(s) holding you down. If y'all are standing on an incline the normal forcefulness would be the reaction force keeping you lot from sinking into the incline AND it would be perpendicular to the incline'south surface.

If yous were to lean on a wall, it is the normal force that keeps you lot from puncturing the wall. In order to have normal force, you must have a contact surface touching something. For example, your shoe on the flooring. The floor exerts a normal force upwardly confronting the shoe while the show exerts a normal force downwardly against the flooring.

Drawing the normal force on an free body diagram.

On a free body diagram, "fbd," the normal strength, "η," is E'er drawn normal to the surface of contact. The management the body is moving and the other forces acting on the body do not change the normal force's direction on a gratis body diagram.

Friction

There are many types of frictional forces. No matter what math formula is used to depict the magnitude of the frictional force, they all betoken in the opposite management of movement, (or the intended motion if there were no friction,) and parallel to the surfaces of contact. The symbol for a frictional force is a cursive "F." (The "F" y'all write does not demand to look exactly like the one below, but it should await "cursive."

We are going to focus in friction due to contact between two surfaces. This frictional force'due south magnitude is a percentage of the normal force pressing the ii surfaces together.

Friction formla

The "coefficient of friction" is the percentage of the normal force. It is institute through experimentation and depends on the nature of the materials in contact. Just because there is a normal strength does not mean that there has to be a frictional force. If you were continuing on a the slickest ice in the world, a normal force would exist keeping your from sinking into the ice simply the frictional force of the "slickest" water ice in the globe might have no measurable value. Beneath is a table of examples frictional coefficients.

Tiptop material	Bottom material	Static coefficient	Kinetic coefficient
ice	ice	0.02	- - -
wood	on dry out wood	0.3	0.ii
atomic number 26	on make clean iron	1.1	0.fifteen
iron	on make clean ,dry, oak	- - -	0.49
graphite	on steel		0.ane
skin	on clean glass	0.9 – one	- - -
Rubber tire	on asphalt	0.7	0.45
Sources: http://hyperphysics.phy-astr.gsu.edu/Hbase/Mechanics/frictire.html http://physics.info/friction https://engineeringlibrary.org/reference/coefficient-of-friction

Notice that some coefficients are greater than one. In the table higher up yous can come across two types of frictional forces exist betwixt the surfaces, static and kinetic friction. Static friction means the two surfaces in contact are not sliding across each other. Kinetic friction means the 2 surfaces are sliding across each other.

The daughter that is standing up in the middle of the playground slide, (right side,) is experiencing static friction between her shoes and the slide because these two surfaces are not moving relative to each other. The girl that is moving downwardly the slide, (left side,) is experiencing kinetic friction between her pants and the slide. This is considering the pants are moving relative to the slide's surface.

In both cases the friction opposes the direction of motion (or the intended direction without friction) and is parallel to surface. The gratuitous body for each girl would wait like the one beneath. The other forces have been dimmed to highlight the frictional strength.

At that place are half dozen basic principles of friction due to contact betwixt surfaces.

Friction acts parallel to the surfaces that are in contact and in the management contrary to the move of the object or to any force tending to produce such motion.
Friction depends on the nature of the materials in contact and the smoothness of their surfaces.
Sliding friction is less than starting friction. Sliding and starting friction are called kinetic and static friction respectively.
Kinetic friction is practically independent of speed.
Friction is practically independent of the area of contact.
Friction is straight proportional to the forcefulness pressing the surfaces together. The reaction force to pressing the surface is the NORMAL force. (See the formula above.)

Drawing the frictional force on a costless body diagram.

Detect that the frictional force'south vector is (1) parallel to the force, (two) opposite the direction of motion -or intended motion.

Below is a box being pushed across a floor AT A CONSTANT VELOCITY.

Beneath are two graphs of the pushing force every bit a office of fourth dimension. The top graphed is plain and the bottom graphed is the same with some added notes.

The box does not move until the pushing strength equals the static friction'south forcefulness value. Because kinetic friction is LESS than static friction, the pushing force'south magnitude drops to the kinetic friction'south value.

I method for determining the coefficient of KINETIC friction. (Does not work for STATIC friction.)

Tension

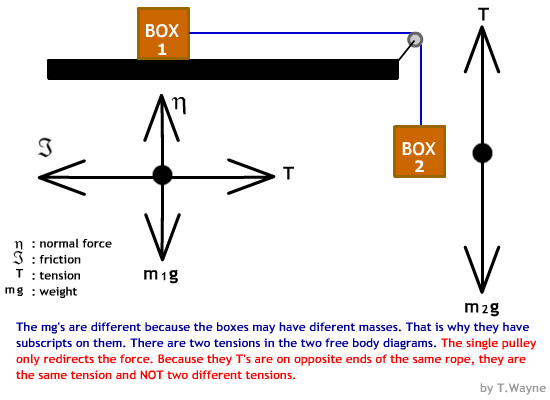
Tension exists in any torso that is pulled by to opposing forces. Typically we talk about ropes and chains as existence in tension simply any torso tin can be in put in tension. Tension is a pair of equal and opposite forces.

In the cartoon above the two 20 North forces correspond the tension in the rope. The forces are equal in magnitude and pulling in contrary directions. A taught rope provides its own action reaction pair. The tension in the rope is said to be "twenty N." In the picture below, the girls' arms are in tension.

One of the clever features of tension and ropes has to do with corners and a single pulley. If the rope passes around a single caster then the direction of the tension is redirected. Assuming the pulley is frictionless (as are all of our pulleys) then the tension's magnitude will remained unchanged. The symbol for tension is "T." In that location is not a formula for tension. Tension's value has to exist either known in the problem or calculated from the other forces.

In society to have a tension your must have a rope or chain. Yous tin also accept a tension when any object is being stretched. Similar the arms of the girls in the photo above.

http://www.nocarnofun.com/wp-content/uploads/2015/04/700HP-Turbo-Cummins-VS-Ford-Powerstroke-On-Super-Swampers-Tug-A-State of war-cl.jpg Image accessed on Jan 1, 2017

In a "tug of war" between 2 trucks, neither truck accelerates. They move at a abiding velocity. The white truck pulls with a measured force of 12,000 Due north. How much force is on the other side of the yellow rope?

Net Force

The "cyberspace" of annihilation is what is left over afterward everything is added and subtracted. Example: When you go hired for a task the employer promises $10 per 60 minutes. But when you go your paycheck your Net pay is $7 per 60 minutes. This is because the federal government, country government and someone called "FICA" took out $ 3. What the employer could have said is that your pay is $10 per hr but your cyberspace pay will be $7 per hour.

When a body is irresolute velocity the net force is not zero. This is because Newton'south 2nd law says an unbalanced force is visually demonstrated by a torso changing its velocity. The "unbalanced" strength described earlier is actually known to physicists as the "net force." Below is an case showing y'all what this looks similar as well as the various free body diagrams. The internet force is represented by the symbol,

F_Internet

The vector that represents the net force does non touch the trunk . This is considering the "internet strength" is non a force that acts on the body. It is the mathematical consequence of adding up all the other forces. That is why information technology is called "net."

Annotation in the blitheness higher up how when the opposite force vectors are the aforementioned length the net force is zero and the body moves with a abiding velocity.[ Examples "C" and "D." ] When the force in one direction are bigger than the forces in the other directions, this is shown on the free body by having i pointer is longer than the other. When this happens the net strength is not zero and the torso accelerates or decelerates. [Examples "A" and "B." ]

The math used to model the situation is derived directly from the the costless body diagram.